
Linear Inequalities and Linear
Equations

Inequalities
The term inequality is applied to any statement involving one of
the
symbols <, >,  ,
,  .
.
Example of inequalities are:
i.
x 1
ii. x + y +
2z > 16
iii. p2
+ q2
1
ii. x + y +
2z > 16
iii. p2
+ q2  1/2
iv. a2 + ab > 1
1/2
iv. a2 + ab > 1
Fundamental
Properties of Inequalities
1. If
a b and c is any real
number, then a + c
b and c is any real
number, then a + c b
+ c.
b
+ c.
For example, -3 -1
implies -3+4
-1
implies -3+4 -1
+ 4.
-1
+ 4.
2. If a b
and c is positive, then ac
b
and c is positive, then ac bc.
bc.
For example, 2 3
implies 2(4)
3
implies 2(4)  3(4).
3(4).
3. If a b
and c is negative, then ac
b
and c is negative, then ac bc.
bc.
For example, 3 9
implies 3(-2)
9
implies 3(-2) 9(-2).
9(-2).
4. If a b
and b
b
and b c,
then a
c,
then a c.
c.
For example, -1/2 2
and 2
2
and 2 8/3
imply -1/2
8/3
imply -1/2 8/3.
8/3.
Solution of
Inequality
By solution of the one variable inequality 2x + 3 7
we mean any
number which substituted for x yields a true statement.
7
we mean any
number which substituted for x yields a true statement.
For example, 1 is a solution of 2x + 3 7
since 2(1) + 3 = 5 and 5
is less than and equal to 7.
7
since 2(1) + 3 = 5 and 5
is less than and equal to 7.
By a solution of the two
variable inequality x - y 5
we mean any
ordered pair of numbers which when substituted for x and y,
respectively, yields a true statement.
5
we mean any
ordered pair of numbers which when substituted for x and y,
respectively, yields a true statement.
For example, (2, 1) is a solution of x - y 5
because 2-1 = 1 and
1
5
because 2-1 = 1 and
1 5.
5.
By a solution of the three
variable inequality 2x - y + z 3
we
means an ordered triple of number which when substituted for x, y and z
respectively, yields a true statement.
3
we
means an ordered triple of number which when substituted for x, y and z
respectively, yields a true statement.
For example, (2, 0, 1) is a
solution of 2x - y + z 3.
3.
A solution of an inequality is said to satisfy the inequality.
For
example, (2, 1) is satisfy x - y 5.
5.
Two or more inequalities, each with the same variables, considered as a
unit, are said to form a system
of inequalities. For example,
Note
that the notion of a system of inequalities is analogous to
that of a solution of a system of equations.
Any solution common to all of the inequalities of a system of
inequalities is said to be a solution of that system of inequalities. A system of inequalities, each of whose members is linear,
is said
to be a system of linear
inequalities.
Geometric
Interpretation of Inequalities
An inequality in two variable x and y
describes a region in
the x-y plane (called its graph), namely, the set of all points whose
coordinates
satisfy the inequality.
The y-axis
divide, the xy-plane into two regions, called half-planes.
- Right
half-plane
The region of points whose coordinates satisfy inequality x > 0.
- Left
half-plane
The region of points whose coordinates satisfy inequality x < 0.
Similarly, the x-axis divides the xy-plane
into two half-planes.
- Upper
half-plane
In which inequality y > 0
is true.
- Lower
half-plane
In which inequality y < 0
is true.
What is x-axis and y-axis? They are simply lines. So, the above
arguments can be applied to any line.
Every line ax + by = c divides the xy-plane into two regions called its
half-planes.
- On one half-plane ax + by > c is true.
- On the other
half-plane ax + by < c is true.
Linear
Equations
One Unknown
A linear equation in one unknown can always be
stated into the
standard form
ax = b
where x is an unknown and a and b are constants. If a is not equal to
zero, this equation has a unique solution
x = b/a
Two Unknowns
A linear equation in two unknown, x and y, can be put
into the form
ax
+ by = c
where x and y are two unknowns and a, b, c are
real numbers. Also, we assume that a and b are no zero.
Solution
of Linear Equation
A solution of the equation consists of a pair of number, u = (k1,
k2),
which satisfies the equation ax + by = c. Mathematically speaking, a
solution consists of u = (k1,
k2) such that ak1 +
bk2 = c. Solution of the equation can be found by
assigning arbitrary values to
x and solving for y OR
assigning arbitrary values to y and solving for
x.
Geometrically, any
solution u = (k1,
k2) of the linear equation ax + by = c
determine a point in
the cartesian plane. Since a and b are not zero, the solution u
correspond precisely to the points on a straight line.
Two Equations in the
Two Unknowns
A system of two linear equations in the two unknowns x
and y is
a1x
+ b1x
= c1
a2x + b2x = c2
Where a1, a2, b1, b2
are
not zero. A pair of
numbers which satisfies both equations is called a
simultaneous solution of the given equations or a solution of the
system of equations.
Geometrically, there are
three cases of a
simultaneous solution
- If the system has exactly one solution, the graph
of the linear
equations intersect in one point.
- If the system has no solutions, the graphs
of the linear
equations are parallel.
- If the system has an infinite number of
solutions, the graphs of
the linear equations coincide.
The special cases (2) and (3) can only occur when the
coefficient of x
and y in the two linear equations are proportional.
OR 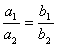 => a1b2
- a2b1
= 0 =>
=> a1b2
- a2b1
= 0 =>  = 0
= 0
The system has no solution when 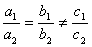
The solution to system
a1x
+ b1x
= c1
a2x + b2x = c2
can be obtained by the elimination process, whereby
reduce the
system to a single equation in only one unknown. This is accomplished
by the following algorithm
ALGORITHM
Step 1
Multiply the two equation by two numbers which
are such
that
the resulting coefficients
of one of the unknown are negative of
each other.
Step 2
Add the equations obtained in Step 1.
The output of this algorithm is
a linear equation in one unknown. This equation may be solved for
that unknown, and the solution may be substituted in one of the
original
equations yielding the value of the other unknown.
As an example, consider
the following system
3x + 2y =
8 ------------ (1)
2x - 5y =
-1 ------------
(2)
Step 1: Multiply
equation (1) by 2 and equation (2) by -3
6x + 4y = 16
-6x + 15y = 3
Step 2: Add equations,
output of Step 1
19y = 19
Thus, we obtain an equation involving only unknown y. we solve for y to
obtain
y = 1
Next, we substitute y =1 in equation (1) to get
x = 2
Therefore, x = 2 and y = 1 is the unique solution to the system.
n Equations in n
Unknowns
Now, consider a system of n linear equations in n
unknowns
a11x1
+ a12x2
+ . . .
+ a1nxn = b1
a21x1 + a22x2
+
. . . + a2nxn = b2
. . . . . . . . . . . . . . . . . . . . . .
. . .
an1x1 + an2x2
+ . . .
+ annxn = bn
Where the aij, bi are real numbers. The
number aij is called the coefficient of xj in the
ith equation, and the number bi is called the
constant of
the ith equation. A list of values for the unknowns,
x1
= k1,
x2
= k2, . . . , xn
= kn
or equivalently, a list
of n numbers
u = (k1, k2,
. .
. , kn)
is called a solution of the system if, with kj substituted
for xj, the left hand side of each equation in fact equals
the right hand side.
The above system is equivalent to the matrix equation.
or, simply we can write A × = B, where A = (aij),
× = (xi), and B = (bi).
The matrix  is called the
coefficient matrix
of the system of n linear equations in the system of
n unknown.
is called the
coefficient matrix
of the system of n linear equations in the system of
n unknown.
The matrix  is called the
augmented matrix
of n linear equations in n unknown.
is called the
augmented matrix
of n linear equations in n unknown.
Note for algorithmic nerds:
we store a system in the computer as its augmented matrix.
Specifically, system is stored in computer as an N × (N+1) matrix
array A, the augmented matrix array A, the augmented matrix of the
system. Therefore, the constants b1, b2, . . . , bn
are respectively
stored as A1,N+1, A2,N+1, . . . , AN,N+1.
Solution of a
Triangular System
If aij = 0 for i > j, then system of
n linear
equations in n unknown assumes the triangular form.
a11x1 + a12x2
+ . . .
+ a1,n-1xn-1 + a1nxn
= b1
a22x2
+
. . . + a2,n-1xn-1 + a2nxn
= b2
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
an-2,n-2xn-2
+
an-2,n-1xn-1 + an-2,nxn-1
+ a2nxn = b2
an-1,n-1xn-1
+ an-1,nxn = bn-1
amnxn = bn
Where |A| = a11a22 . . . ann;
If none of the diagonal entries a11,a22, .
.
., ann is zero, the system has a
unique solution.
Back Substitution
Method
we obtain the solution of a triangular system by the
technique of
back substitution, consider the above general triangular system.
1. First, we solve the last equation for the last unknown, xn;
xn
= bn/ann
2. Second, we substitute the value of xn in the next-to-last
equation and solve it for the next-to-last unknown, xn-1:
 .
.
3. Third, we substitute these values for xn and xn-1
in the third-from-last equation and solve it for the third-from-last
unknown, xn-2 :
 .
.
In general, we determine xk by substituting the previously
obtained values of xn, xn-1, . . . , xk+1
in the kth equation.
 .
.
Gaussian Elimination
Gaussian elimination is a method used for finding the
solution of a
system of linear equations. This method consider of two parts.
- This part consists of step-by-step putting the
system into
triangular system.
- This part consists of solving the triangular
system by back
substitution.
x - 3y - 2z = 6 --- (1)
2x - 4y + 2z = 18 --- (2)
-3x + 8y + 9z = -9 --- (3)
First Part
Eliminate first unknown x from the equations 2 and 3.
(a) multiply -2 to equation (1) and add it to equation (2). Equation
(2) becomes
2y + 6z
= 6
(b) Multiply 3 to equation (1) and add it to equation (3). Equation (3)
becomes
-y + 3z = 9
And the original system is reduced to the system
x - 3y - 2z = 6
2y + 6z = 6
-y + 3z
= 9
Now, we have to remove the second unknown, y, from new equation 3,
using only the new equation 2 and 3 (above).
a, Multiply equation (2) by 1/2 and add it to equation (3). The
equation (3) becomes 6z = 12.
Therefore, our given system of three linear equation of 3 unknown
is reduced to the triangular system
x - 3y - 2z = 6
2y + 6z = 6
6z = 12
Second Part
In the second part, we solve the equation by
back substitution and
get
x = 1, y = -3, z = 2
In the first stage of the algorithm, the coefficient of x in the first
equation is called the pivot,
and in the second stage of the algorithm,
the coefficient of y in the second equation is the point. Clearly, the
algorithm cannot work if either pivot is zero. In such a case one must
interchange equation so that a pivot is not zero. In fact, if one would
like to code this algorithm, then the greatest accuracy is attained
when the pivot is as large in absolute value as possible. For
example,
we would like to interchange equation 1 and equation 2 in the original
system in the above example before eliminating x from the second and
third equation.
That is, first step of the algorithm transfer system as
2x - 4y + 2z = 18
x - 4y + 2z = 18
-3x + 8y + 9z = -9
Determinants and systems of linear
equations
Consider a system of n linear equations in n
unknowns. That is, for the following system
a11x1
+ a12x2
+ . . .
+ a1nxn = b1
a21x1
+ a22x2
+
. . . + a2nxn = b2
. . . .
. . . . . . . . . . . . . . . . . . . . .
an1x1
+ an2x2 + . . .
+ annxn = bn
Let D denote the determinant of the matrix A +(aij) of
coefficients; that is, let D =|A|. Also, let Ni denote the
determinants of the matrix obtained by replacing the ith
column of A by the column of constants.
Theorem. If D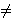 0, the above system of linear equations
has the unique solution
0, the above system of linear equations
has the unique solution  .
.
This theorem is widely known as Cramer's
rule. It is important to note
that Gaussian elimination is usually much more efficient for solving
systems of linear equations than is the use of determinants.


![]()
![]()
![]()
![]()
 ,
,  .
.  1
1  1/2
1/2 b and c is any real
number, then a + c
b and c is any real
number, then a + c b
+ c.
b
+ c. -1
implies -3+4
-1
implies -3+4 -1
+ 4.
-1
+ 4. b
and c is positive, then ac
b
and c is positive, then ac bc.
bc. 3
implies 2(4)
3
implies 2(4)  3(4).
3(4). b
and c is negative, then ac
b
and c is negative, then ac bc.
bc. 9
implies 3(-2)
9
implies 3(-2) 9(-2).
9(-2). b
and b
b
and b c,
then a
c,
then a c.
c. 2
and 2
2
and 2 8/3
imply -1/2
8/3
imply -1/2 8/3.
8/3.
 7
we mean any
number which substituted for x yields a true statement.
7
we mean any
number which substituted for x yields a true statement. 7
since 2(1) + 3 = 5 and 5
is less than and equal to 7.
7
since 2(1) + 3 = 5 and 5
is less than and equal to 7. 5
we mean any
ordered pair of numbers which when substituted for x and y,
respectively, yields a true statement.
5
we mean any
ordered pair of numbers which when substituted for x and y,
respectively, yields a true statement. 5
because 2-1 = 1 and
1
5
because 2-1 = 1 and
1 5.
5. 3
we
means an ordered triple of number which when substituted for x, y and z
respectively, yields a true statement.
3
we
means an ordered triple of number which when substituted for x, y and z
respectively, yields a true statement.  3.
3. 5.
5. 0
0 0
0 4
4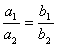
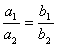 => a1b2
- a2b1
= 0 =>
=> a1b2
- a2b1
= 0 =>  = 0
= 0

 is called the
coefficient matrix
of the system of n linear equations in the system of
n unknown.
is called the
coefficient matrix
of the system of n linear equations in the system of
n unknown. is called the
augmented matrix
of n linear equations in n unknown.
is called the
augmented matrix
of n linear equations in n unknown.  .
. .
. .
.
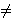 0, the above system of linear equations
has the unique solution
0, the above system of linear equations
has the unique solution  .
.![]()