
Vectors and Matrices

A
vector, u, means a list
(or n-tuple) of numbers:
u = (u1,
u2, . . . , un)
where ui are called the components of u. If all the ui
are zero i.e., ui = 0, then u is
called the zero vector.
Given vectors u and v are equal i.e., u = v, if they have the same
number of components and if corresponding components are equal.
Addition of Two
Vectors
If two vectors, u and v, have the number of components,
their sum, u +
v, is the vector obtained by adding corresponding components from u and
v.
u + v = (u1, u2,
. . . , un) + (v1, v2, . . . , vn)
= (u1 + v1 + u2
+ v2, . . . , un + vn)
Multiplication of a
vector by a Scalar
The product of a scalar k and a vector u i.e., ku, is the
vector obtained by multiplying each component of u by k:
ku
= k(u1, u2,
. . . , un)
= ku1,
ku2, . . . , kun
Here, we define -u =
(-1)u
and u-v = u +(-v)
It is not difficult to see k(u
+ v) = ku + kv where k is a scalar and u and
v are vectors
Dot Product and Norm
The dot
product or inner product
of vectors u = (u1, u2,
. . . , un) and v = (v1, v2,
. . . , vn)
is denoted by u.v and
defined by
u.v = u1v1
+ u2v2 + . . . +
unvn
The norm or length of a vector, u,
is denoted by ||u|| and
defined by
Matrices
Matrix, A, means a rectangular array of numbers
A = 
The m horizontal n-tuples are called the rows of A, and the n vertical
m-tuples, its columns. Note that the element aij, called the
ij-entry, appear in the ith row and the jth
column.
In algorithmic (study of
algorithms), we like to write a matrix A as A(aij).
Column Vector
A matrix with only one column is called a column
vector
Zero Matrix
A matrix whose entries
are all zero is called
a zero matrix and denoted
by 0.
Matrix Addition
Let A and B be two matrices of the same size. The sum of A and B
is
written as A + B and obtained by adding corresponding elements from A
and B.
A+B = 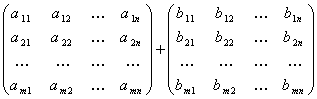
= 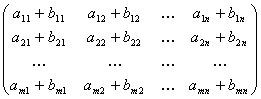
Scalar Multiplication
The product of a scalar k and
a matrix A, written kA or Ak, is the matrix obtained by
multiplying each element of A by k.
kA = k 
=

Here, we define -A = (-1)A
and A - B = A +
(-B). Note that -A is
the negative of the matrix A.
Properties of Matrix
under Addition
and Multiplication
Let A, B, and C be matrices of same size and let k and l be scalars. Then
- (A + B) + A + (B + C)
- A + B = B + A
- A + 0 = 0 + A = A
- A + (-A) = (-A) + A = 0
- k(A + B) = kA + kB
- (k + l)A = kA + lA
- (kl)A
= k(lA)
- lA = A
Matrix Multiplication
Suppose A and B are two matrices such that the number
of columns of A
is equal to number of rows of B. Say matrix A is an m×p matrix
and matrix B is a p×n matrix. Then the product of A and B is the
m×n matrix whose ij-entry is obtained by multiplying the elements
of the ith row of a by the corresponding elements of the jth column of
B and then adding them.
It is important to note that if the number of columns of A is not equal
to the number of rows of B, then the product AB is not defined.
Properties of Matrix
Multiplication
Let A, B, and C be matrices and let k
be a scalar. Then
- (AB)C = A(BC)
- A(B+C) = AB + AC
- (B+C)A = BA + CA
- k(AB) = (kB)B = A(kB)
Transpose
The transpose of a matrix A is obtained by writing the
row of A, in
order, as columns and denoted by AT. In other
words, if A - (Aij), then B = (bij) is
the transpose of A if bij - aji for all i and j.
It is not hard to see that if A
is an m×n matrix,
then AT
is an n×m
matrix.
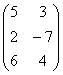
For example if A = 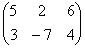 , then AT
=
, then AT
= 
Square Matrix
If the number of rows and the number of columns
of any matrix are
the same, we say matrix is a square matrix, i.e., a square matrix has
same number of rows and columns. A square matrix with n rows and n
columns is said to be order n and is called an n-square matrix.
The main diagonal, or
simply diagonal, of an
n-square matrix A = (aij)
consists of the elements a11, a22, a33,
. . . , amn.
Unit Matrix
The n-square matrix
with 1's along the main diagonal and 0's elsewhere
is called the unit matrix and usually denoted by I.
Why unit matrix?
The unit matrix plays
the same role in matrix multiplication as the
number 1 does in the usual multiplication of numbers.
AI = IA = A
for any square matrix A.
So what dude?
We can form powers of a
square matrix X by defining
X2 = XX
X3 = X2X,
XXX, . . .
X0 = I
Big deal!
We can also form
polynomial in X. That is, for any polynomial
f(x) = a0
+ a1x + a2x2 + .
. . + anxn
We define f(x) to be
the matrix
f(x) = a0I
+ a1x + a2x2 + .
. . + anxn
Note that in the case
that f(A) is the zero matrix, then matrix A said
to be a zero of the polynomial f(x) or a root of the polynomial
equation f(x) = 0.
Now you're talking !!!!
Invertible Matrices
A square matrix A is said to be invertible if there exists
a matrix B with the property AB = BA = I (Identity Matrix). Such a
matrix B is unique and it is called the matrix of A and is
denoted by A-1. Here, the important
observation is that B is
the inverse of A if and only if A is the matrix of B. It is known that
AB = I if and only if
BA = I; hence it is necessary to test only one
product to determine whether two given matrices are inverse.
Determinants
To each n-square matrix A = (aij), we assign
a specific
number called the determinants of A and denoted as
|A|
= del(A)
= 
where an n by
n arrays of numbers enclosed
by
straight lines is called a determinant of order n.
It is important to note that n by n array of numbers enclosed by
straight line (see above) is NOT
a matrix but denotes the number that
the determinant function assigns to the enclosed array of numbers,
i.e., the enclosed square matrix.
The determinant of order one
is |a11|
= a11
The determinant of order two
is  = a11a22 - a12a21
= a11a22 - a12a21
The determinant of order
three is  = a11a22a32+ a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32
= a11a22a32+ a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32
The determinant of order fo... You get the picture !
General Definition
of Determinant
The general definition of a determinant of order
n is as follows
det(A) = 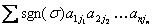
where the sum is
over all possible permutations 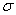 = (j1, j2 , . . . , jn
) of (1, 2, . . . , n). Here
sgn(
= (j1, j2 , . . . , jn
) of (1, 2, . . . , n). Here
sgn(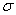 )
equals plus or minus one according as an even or an odd number of
interchanges are required to change
)
equals plus or minus one according as an even or an odd number of
interchanges are required to change 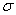 so that its numbers are in the usual order.
so that its numbers are in the usual order.
An important property of the determinant function is
Lemma. For any two
n-square matrices A and B,
det(AB) = det(A) . det(B).
In simple words the lemma say that the determinant function is
multiplicative.
An important point in the context of invertible matrices and
determinant is
Lemma. A square matrix is
invertible if and only
if it has a nonzero determinant.
A good news and a bad news:
If you're an under graduate, you're done here! now goto CLR- If you're graduate and
interested in theoretical Computer Science its time to go and find some
good on matrix theory. (You'll need this shit for Linear Programming,
for example).


![]()
![]()
![]()
![]()
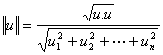

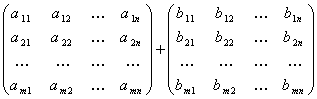
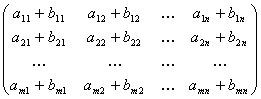


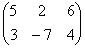 , then AT
=
, then AT
= 

 = a11a22 - a12a21
= a11a22 - a12a21 = a11a22a32+ a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32
= a11a22a32+ a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32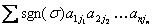
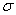 = (j1, j2 , . . . , jn
) of (1, 2, . . . , n). Here
sgn(
= (j1, j2 , . . . , jn
) of (1, 2, . . . , n). Here
sgn(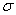 )
equals plus or minus one according as an even or an odd number of
interchanges are required to change
)
equals plus or minus one according as an even or an odd number of
interchanges are required to change 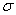 so that its numbers are in the usual order.
so that its numbers are in the usual order.![]()