![]()
The Two-Ears Theorem
![]()
![]()
![]()
The two-ear theorem was developed and proved by Gary H. Meisters in 1975.
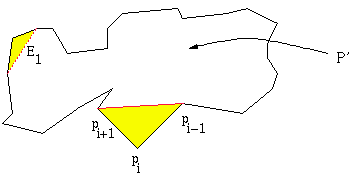
Ear
A principal vertex pi of a simple polygon P is called an ear if the diagonal (pi-1, pi+1) that bridges pi lies entirely in P. We say that two ears pi and pj are non-overlapping if the interior of triangle (pi-1, pi, pi+1) does not intersect the interior of triangle (pj-1, pj, pj+1)
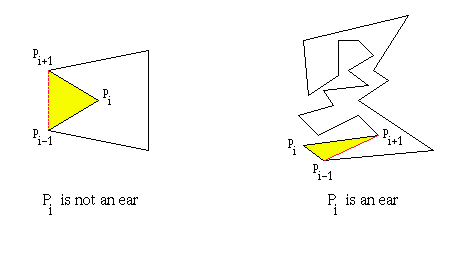
Examples of Ear(s)
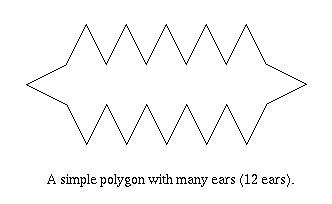
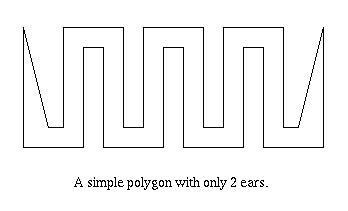
Theorem Except for triangles, every simple polygon has at least two non-overlapping ears.
Meisters' Proof
The proof is by Induction on the number of vertices, n, in the simple polygon, P.
Base case
When n = 4. The simple polygon is a quadrilateral and has two ears, E1 and E2, as shown below.
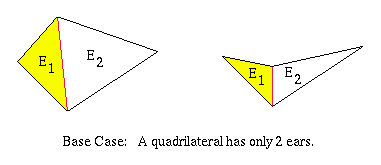
Induction
Let P be a simple polygon with at least 4 vertices. Consider vertex pi is a vertex of P where the interior angle formed by pi-1, pi, and pi+1 is less than 180o.
There are two case. Either polygon P has an ear at vertex pi or it does not (i.e. P does not have ear at an ear at vertex, pi).
Case 1 Polygon P has an ear at pi. If this ear is removed, the resulting polygon P' is a simple polygon with more than three vertices, but with one less vertex than P. By the induction hypothesis, there are two non-overlapping ears E1 and E2 for P'. Since they are non-overlapping, at least one of these two ears, say E1, is not at either of the vertices pi-1 or pi+1. Since all ears of P' are also ears of P, polygon P has two ears: E1 and the ear at pi.
Case 2 Polygon P does not have an ear at pi. So, the triangle formed by pi-1, pi, and pi+1 contains at least one vertex of P in its interior. Let q be the vertex in the interior of this triangle such that the line L through q and parallel to the line through pi-1 and pi+1 is as close to pi as possible.
Let a and b be the points of intersection of line L with the polygon edges (pi, pi+1) and (pi-1, pi), respectively. The triangle formed by pi, a, and b does not contain in its interior any vertex of P (or else our choice of vertex q would be incorrect).
The line segment Q from vertex q to pi can be constructed without intersecting any edges of P. Line segment Q divides P into two simple polygons: P1 (that contains vertices pi, pi+1,..., q) and P2 (that contains vertices pi, pi-1,..., q).
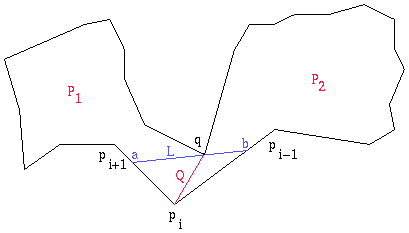
There are two sub-cases of case 2.
Case 2a Polygon P1 is a triangle. So, P1 is an ear for polygon P. By the induction hypothesis, polygon P2 must have at least two non-overlapping ears, E1 and E2 (or else it too would be a triangle and polygon P would have only four vertices). Since they are non-overlapping, at least one, say E1, is at neither vertices pi nor q. E1 does not overlap with the ear formed by polygon P1, so it is the second ear in polygon P.
Case 2b
Polygon P1 is not a
triangle. So, by the induction hypothesis, polygon P1 has
two ears, E11 and E12 and polygon P2
has two ears, E21 and E22. Since they are
non-overlapping, at least one of the ears in P1, say E11,
is not at vertex pi or q. Similarly, at least one of
the ears in P2, say E21, is not at vertex
pi or q. These two ears, E11 and
E21 will be non-overlapping ears for polygon P
This completes the proof.
An O(kn)-time Algorithm
Following algorithm finds an ear in the simple polygon P :
Alogrithm FindEar(P)
1. i = 0
2. ear not found = true
3. while ear not found
4. if pi is convex then
5. if triangle pi-1, pi, and pi+1 contains no concave vertex then
6. ear not found = false
7. if ear not found then
8. i = i + 1
9. return pi
Correctness [2]
By the Two-Ears Theorem, simple polygon P has at least 2 ears if the number of vertices is > 3. If the number of vertices is 3, then P is a triangle and forms 1 ear. By the definition of a polygon, there is always at least 1 ear in P for the algorithm to find.
To complete the proof of correctness, it suffices to prove the following lemma :
Lemma If a convex vertex pi is not an ear, then the triangle formed by pi-1, pi, and pi+1 contains a concave vertex.
Proof
If pi is not an ear, then the triangle
formed by pi-1, pi, and pi+1
contains a vertex. Let pj be the vertex in the interior of
this triangle (pi-1, pi, pi+1)
such that the line L through pj and parallel to the
line through pi-1 and pi+1
is as close to pi as possible. Let a and b be
the points of intersection of line L with the polygon edges (pi,
pi+1) and (pi-1, pi)
respectively. Triangle (a, pi, b) has no
vertices in its interior and lies entirely inside P. Vertices pj-1
and pj+1 must lie on the opposite side of line L,
so pj is a concave vertex.
This completes the proof of lemma.
This completes the proof of correctness.
Clearly, lines 1 and 2 run in constant time. The loop in line 3 is executed at most n - 2 times, which occurs when P has only 2 ears and is similar to this :
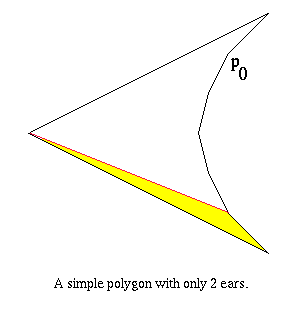
The starting vertex of above algorithm is p0. (i=0 at line 1). If the vertices are sorted in clockwise order, the algorithm would find first ear shown in yellow. The number of vertices scanned to find this ear is n - 2, where n is the number of vertices in P. Obviously, line 4 runs in constant time. Line 5 may require O(k) time where k - 1 is the number of concave vertices in P since it is possible that all concave vertices are checked for being in triangle (pi-1, pi, pi+1). Lines 6, 7, 8, and 9 all run in constant time. Since line 5 executed in time proportional to n in the worst case, the algorithm runs in O(kn) time. However, since k - 1 is the number of concave vertices, the algorithm can be as bad as O(n2).
An O(n)-time Algorithm
This recursive algorithm was proposed by Hossam ElGindy and Godfried T. Toussaint.
The input of the algorithm is a good sub-polygon GSP and a vertex pi. Initially, the algorithm FindAnEar is called with the simple polygon P and any vertex of P.
Algorithm FindAnEar (GSP, pi)
1. if pi is an ear then
2. return pi
3. Find a vertex pj such that (pi, pj) is a diagonal of GSP.
Let GSP' be the good sub-polygon of GSP formed by (pi, pj).
Re-label the vertices of GSP' so that pi = p0 and pj = pk-1
(or pj = p0 and pi = pk-1 as appropriate) where k is the number
of vertices of GSP'.
4. FindAnEar(GSP', floor(k/2))
The correctness of the algorithm depends upon the following three Lemmas 1, 2, and 3.
Lemma 1 A good sub-polygon has at least one proper ear.
Proof
Let (pi, pj) be the
cutting edge of GSP. By the
Two-Ears Theorem GSP has at least two non-overlapping ears.
Vertices pi and pj cannot be the only ears
of GSP since these would overlap. Thus some other vertex of GSP
is an ear and it is a proper ear.
This completes the proof of lemma 1.
Lemma 2 A diagonal of a good sub-polygon GSP splits GSP into one good sub-polygon and one sub-polygon that is not good.
Proof
GSP contains exactly one edge, the cutting edge, which
is not an edge of P. The cutting edge is entirely contained in one of
the sub-polygons formed by the diagonal. Then the other sub-polygon is a good
sub-polygon since it consists of edges of P and the diagonal which
becomes its cutting edge.
This completes the proof of lemma 2.
Lemma 3 If vertex pi is not an ear then there exists a vertex pj such that (pi, pj) is a diagonal of P.
Proof
Given a vertex pi which is not an ear we will show how to find a vertex pj such that (pi, pj) is a diagonal. Construct a ray, ray(pi), at pi that bisects the interior of angle (pi-1, pi, pi+1). Find the first intersection point of ray(pi) with the boundary of P. Note that this is done simply by testing each edge of the polygon for intersection with ray(pi). Let y be the intersection point on edge (pk, pk+1). Point y must exist and y <> pi-1 or pi+1. Note that the line segment (pi, y) lies entirely inside P. Thus if y is a vertex then (pi, y) is a diagonal. Suppose y is not a vertex. Then pk+1 and pi-1 lie in one of the half-planes defined by ray(pi), and pk and pi+1 lie in the other. We will show that if triangle (pi, y, pk+1) does not contain a vertex pj such that (pi, pj) is a diagonal of P then triangle (pi, y, pk) does.
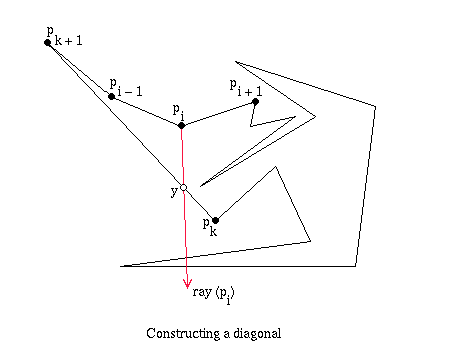
Let R = {pr in P such that pr
lies in triangle (pi, y, pk+1),
k+1 < r < i}. If R = NULL then by the
Jordan Curve Theorem and the fact that line segment (pi,
y) lies entirely inside P, the interior of triangle (pi,
y, pk+1) is empty. If pk+1
<> pi-1 then (pi, pk+1)
is a diagonal. Otherwise let z = pi-1. If R
= NULL then for all pr in R compute angle (y,
pi, pr) and let z be the vertex
that minimizes this angle. By choice of z, the interior of triangle (pi,
y, z) is empty. Thus if z <> pi-1
then (pi, z) is a diagonal. Hence if no diagonal has
been found thus far then z = pi-1. Similarly
define S = {ps in P such that ps
lies in triangle (pi, y, pk), i
< s < k}. If S = NULL, the interior of triangle (pi,
y, pk) is empty and if pk <> pi+1
then (pi, pk) is a diagonal. Define w
analogously to z; that is, either w = pi+1
or w is the vertex that minimizes angle (y, pi,
ps). By choice of w the interior of triangle (pi,
y, w) is empty. We will show that w <> pi+1
and then it follows that (pi, w) is a diagonal.
Recall that z = pi-1 so that triangle (pi,
y, pi-1) is empty. Assume that w = pi+1
so that triangle (pi, y, pi+1)
is empty.
Case 1 When pi is a
convex vertex.
Since pi is not an ear, at least one vertex of P lies
in triangle (pi-1, pi, pi+1).
Suppose y lies outside of triangle (pi-1, pi,
pi+1). Since triangle (pi, y,
pi-1) and triangle (pi, y,
pi+1) are empty then so is (pi-1,
pi, pi+1) which is a contradiction.
Suppose y lies inside of triangle (pi-1, pi,
pi+1). Since triangle (pi, y,
pi-1) is empty, pk+1 does
not lie in triangle (pi, y, pi-1).
Similarly, pk does not lie in triangle (pi,
y, pi+1). But then there is no place for
segment pk pk+1.
Case 2 When pi is not a convex vertex.
Since z = pi-1 , pk does not
lie between rays piy and pi pi-1.
Similarly, pk+1 does not lie between rays pi
y and pi pi+1. Since pk+1
lies in the same half-plane defined by ray(pi) as
pi-1, and pk and pi+1
lie in the other there is no place for segment pkpk+1
This completes the proof of lemma 3.
This completes the proof of correctness.
Line 1 of FindAnEar can be done in O(n) time where n is the number of vertices in GSP. Line 2 takes constant time. Line 3 can be done in O(n) time as well. On the first two calls to FindAnEar, GSP has O(n) vertices. Consider any subsequent call. Let k be the number of vertices in GSP. We have i = floor(k/2) and (p0, pk-1) the cutting edge of GSP. Consider line 3. If 0 <= j <= i-2 then GSP' = (pj, pj+1, ..., pi). Otherwise, i+2 <= j <= k-1 and GSP' = (pi, pi+1, ..., pj). In either case, GSP' contains no more than floor(k/2) + 1 vertices.
[1] ElGindy, H., H. Everett, and G.T. Toussaint, Slicing an ear using prune-and-search, Pattern Recognition Letters. September 1993, 719-722.
[2] Kong, X., H. Everett, and G.T. Toussaint, The Graham scan triangulates simple polygons, Pattern Recognition Letters. November 1990, 713-716.
![]()