
From a Regular Expression to an NFA

Thompson's construction is an NFA from a regular expression.
The Thompson's construction is guided by the syntax of the regular expression
with cases following the cases in the definition of regular expression.
-
ε
is a regular expression that denotes {ε},
the set containing just the empty string.
diagram
where i is a new start state and f is a new accepting state. This NFA
recognizes {ε}.
- If a is a symbol in the alphabet, a
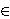 ∑,
then regular expression 'a' denotes {a} and the set containing just 'a'
symbol.
∑,
then regular expression 'a' denotes {a} and the set containing just 'a'
symbol.
diagram
This NFA recognizes {a}.
- Suppose, s and t are regular expressions denoting L{s} and L(t)
respectively, then
- s/r is a regular expression denoting L(s) L(t)
- st is a regular expression denoting L(s) L(t)
diagram
- s* is a regular expression denoting L(s)*
diagram
- (s) is a regular expression denoting L(s) and can be used for putting
parenthesis around regular expression
Example: Use above algorithm, Thompson's construction, to construct NFA for
the regular expression r = (a|b)* abb.
First constant the parse tree for r = (a|b)* abb.
figure
figure
figure
figure
figure
We have r5 = (a|b)*
figure
figure
We get r7 =(a|b)* a
Similarly for r8 and r10 - use case 2
figure
figure
And get r11 by case 3b
figure
We have r = (a|b)*abb.


![]()
![]()