4. Anisotropy in Liquid Crystals
Prev		Next
The uniaxial symmetry around the director in the LC phase leads to an anisotropy in many physical properties. For example, the refractive index, the dielectric permittivity, the magnetic susceptibility, viscosity and conductivity have a different value parallel to the director n and perpendicular to it.
Optical Anisotropy of Liquid Crystals
The anisotropy of LCs causes light polarized along the director n to propagate at a different velocity than light polarized perpendicular to it. Therefore, LCs are birefringent. A uniaxial LC has two principal refractive indices, ordinary refractive index no and extraordinary refractive index ne. The first one, no, is measured for the light wave where the electric vector vibrates perpendicular to the optical axis (ordinary wave) (Fig.5a). The index ne is measured for the light wave where the electric vector vibrates along the optical axis (extraordinary wave) (Fig.5b). Then the birefringence is given by Δn = ne - no. (a) (b) Figure 5. Light propagation in LCs along and normal to optical axis: (a) ordinary beam; (b) extraordinary beam; ne - extraordinary refractive index; no - ordinary refractive index Usually, ne > no and, therefore, Δn is positive and varies in the range from values close to zero to about 0.4. In the case of uniaxial LCs the optic axis coincides with the director n. The indices no and ne are measured for the light propagating along or normal to the optical axis. 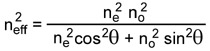In the case when the direction of the light propagation is tilted with respect to the optical axis (Fig.6), the refractive index for the ordinary wave is equal to no, but the refractive index for the extraordinary wave is equal to some effective value given by where θ is an angle between the optical axis and the light propagation direction. Then birefringence is Δn = neff - no. Figure 6. Light propagating at some angle θ to optical axis In the case of propagation along the optical axis, the refractive index is no for both modes, ordinary and extraordinary. More formally, the refractive index is related to the response of matter to an electric field. Then, in general, refractive index depends on dielectric permittivity ε depending on the frequency of the applied field. When considering LCs we are interested in the optical frequency range, where na2 = εa, a = x, y, z, where na is the refractive index along the a direction. 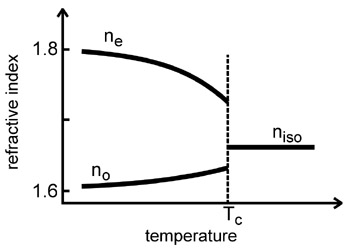In general, birefringence Δn of LCs decreases as the wavelength of the incident light or the temperature increases, Δn ∝ S(T). Figure 7. Temperature dependence of refractive index: Tc - clearing temperature; niso - refractive index of isotropic liquid The unpolarized light incident upon a LC is splitted to the ordinary and extraordinary waves, which travel with different velocities through the material. They emerge from the LC with some phase difference that depends on the thickness of material d Δφ = 2π Δn d/λ, where λ is a light wavelength. Thus, varying the thickness of the LC material produces different phase shifts and the outcoming light polarizations.
Prev Director	Home Up	Next Dielectric anisotropy of LCs